第四章 线性网络的基本定理

4-1、试用叠加定理求图4—1所示电路中通过的电流R₃支路的电流I₃及理想电流源的端电压U。图中I_s=2A，U_s=2V，R₁=3Ω，R₂= R₃=2Ω。

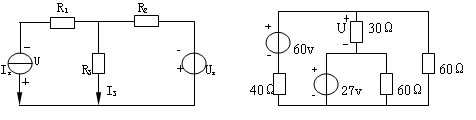
图4—1 图4—2

4-2、用叠加定理求图4—2所示电路的电压U。

4-3、用叠加定理求图4—3所示电路中的开路电压U_oc.

4-4、电路如图4—4所示，当开关S合在1时，电流表读数为40mA，合在2时，电流表读数为190mA ，求S合在3时电流表的读数。

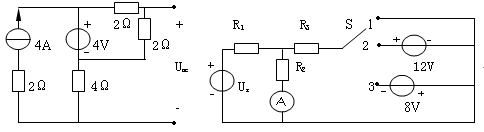
图4—3 图4—4

4-5、用齐性定理求图4—5所示电路中的电流I。

4-6、用叠加定理求图4—6所示电路中的U。

图4—5 图4—6

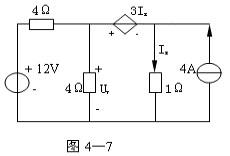
4-7、用叠加定理求图4—7所示电路中的U_y及I_x.

4-8、求图4—8所示各电路的戴维南等效电路。

4-9、图4—9a所示的线性含源二端网络，经测量得知端口的伏安特性如图4—9b所示，求其戴维南等效电路。

4-10、用戴维南定理求图4—10所示各电路中的电压U或电流I。

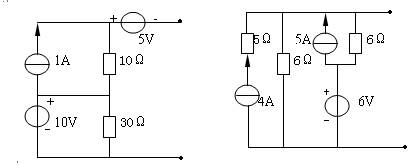
（a） （b）

图4—8

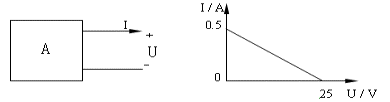
（a） （b）

图4—9

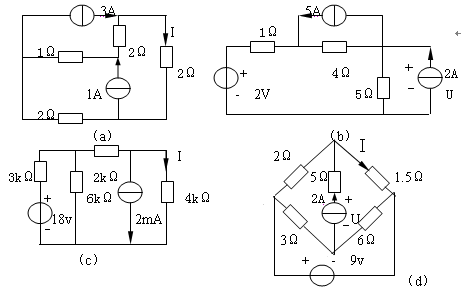
图4—10

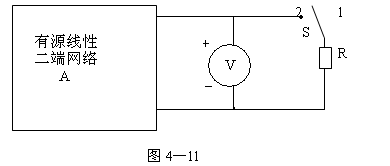
4-11、在图4—11中，为了求得网络A的戴维南等效电路，先将开关s置于1的位置，电压表的读数即为U_oc，再将开关置于2的位置，电压表的读数为U₁，试证明网络A的戴维南等效电阻为R_eq=(U_oc/U₁-1)R.

4-12、求图4—12所示各电路的戴维南等效电路。

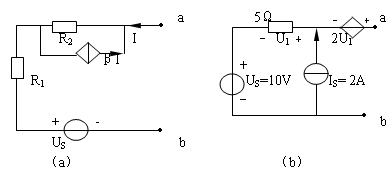
图4—12

4-13、用戴维南定理求图4—13电路中的电压U

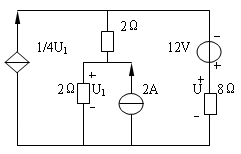
图4—13

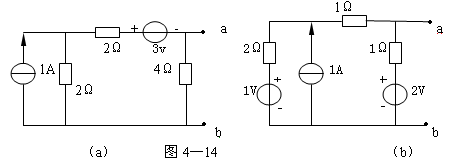
4-14、求图4—14所示各电路的诺顿等效电路。

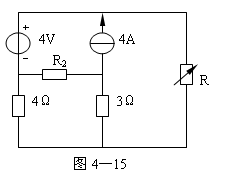
4-15、图4—15电路中，R₂为定值，R可变，当R=2Ω时，R上可获得最大功率，试确定电阻R₂的值，并求R上获得的最大功率。